homothety
Appearance
English
[edit]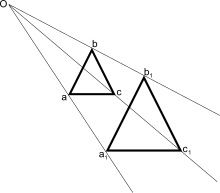
Etymology
[edit]From Ancient Greek ὁμο- (homo-, “same”) + θέσις (thésis, “setting, placement, arrangement”).
Pronunciation
[edit]Noun
[edit]homothety (plural homotheties)
- (mathematics, geometry) An isotropic scaling transformation of an affine space with a single fixed point.
- 1927, Henry George Forder, The Foundations of Euclidean Geometry[1], page 178:
- The product of two homotheties with the same centre is a homothety with that centre.
- 1972, Clayton W. Dodge, Euclidean Geometry and Transformations, published 2004, page 106:
- One cannot obtain all similarity mappings from products of homotheties alone, but they are necessary and basic to similarities.
- 2011, Agustí Reventós Tarrida, Affine Maps, Euclidean Motions and Quadrics, Springer Undergraduate Mathematics Series, page 69:
- Since homotheties are determined by the fixed point, called the center of the homothety, and by the similitude ratio λ, we shall denote by hP,λ the homothety with center P and similitude ratio λ.
- (commutative algebra, Bourbakist) A homomorphism from a module over a ring to itself of the form for some fixed (especially when ; is said to be the ratio of the homothety, by analogy with the geometric case).
Synonyms
[edit]- (isotropic scaling transformation with a fixed point): homothecy, homogeneous dilation, homothetic transformation







