Greco-Latin square
Appearance
English
[edit]Noun
[edit]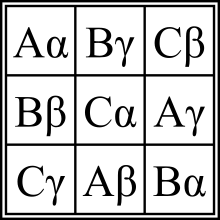
Greco-Latin square (plural Greco-Latin squares)
- A form of Latin square formed by the superposition of two Latin squares that do not lead to the same composite value appearing in any of the squares of the result.
- 2013, Natalia Juristo, Ana M. Moreno, Basics of Software Engineering Experimentation, page 381:
- Bose and Shrikhande then applied these rules and were able to build a Greco-Latin square of order 22. This disproved Euler's conjecture, as 22 is an even number not divisible by four.
- 2018, Reza Hoshmand, Design of Experiments for Agriculture and the Natural Sciences, page 48:
- Table 3.3.3.1 shows a Greco-Latin square with four treatments.
- 2012, Jason Rosenhouse, Laura Taalman, Taking Sudoku Seriously, page 43:
- Since we now have repeated ordered pairs, the square above is not a Greco-Latin square.
