Bézier curve

English

Animation of the construction of a quadratic Bézier curve. The parameter t ∈ [0,1] defines by linear proportion the positions of the endpoints of the green line along the lines P₀P₁ and P₁P₂ as well as the point along the green line that is on the Bézier curve.

A Bézier curve with four control points (a cubic Bézier curve)

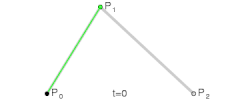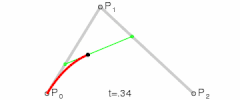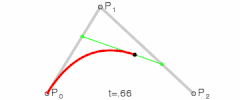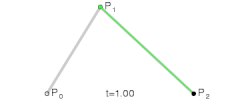
Etymology

Probably a calque of French courbe de Bézier. Named after Renault engineer Pierre Bézier who popularized the curves developed earlier by Paul de Casteljau and used them to design curves for the bodywork of cars.

Pronunciation

• IPA^(key): /ˈbɛz.i.eɪ/ + curve

Noun

Bézier curve (plural Bézier curves)

1. (mathematics, computer graphics) A type of parametric curve defined by a set of control points, two of which are the ends of the curve, while the others determine its shape. [From 1960s.]

   Synonym: bezier

   Bézier curves are applied, for example in computer graphics and animation, to produce smooth, infinitely scalable curves.

   • 2003, Samuel R. Buss, 3D Computer Graphics: A Mathematical Introduction with OpenGL, Cambridge University Press, page 163:

     So, instead, it is often better to combine multiple Bézier curves to form a longer, more complicated curve called a piecewise Bézier curve.
     This section discusses how to join Bézier curves together – especially how to join them so as to preserve continuity and smoothness (i.e., continuity of the first derivative).

   • 2008, T. Theoharis, G. Papaioannou, N. Platis, N. M. Patrikalakis, Graphics & Visualization: Principles and Algorithms‎^[1], Taylor & Francis (A K Peters / CRC Press), page 193:

     The initial points p₀, p₁, and p₂ are called control points of the Bézier curve. […] The process outlined above for the generation of a quadratic Bézier curve from its three control points can be generalized for more control points in a straightforward manner.

   • 2012, Frank Klawonn, Introduction to Computer Graphics: Using Java 2D and 3D, 2nd edition, Springer, page 151:

     When an affine transformation is applied to the control points, the resulting Bézier curve with respect to the new control points coincides with the transformed Bézier curve. Therefore, Bézier curves are invariant under affine transformations like rotation, translation or scaling. Bézier curves are also symmetric with respect to their control points.

Related terms

• bezier
• Bézier coefficient
• Bézier spline
• Bézier surface
• Bézier triangle

 

Translations

kind of parametric curve

• Chinese:

  Mandarin: 貝茲曲線 / 贝兹曲线 (zh) (Bèizī qǔxiàn)

• Czech: Bézierova křivka f
• Finnish: Bézier-käyrä
• French: courbe de Bézier f
• German: Bézierkurve f
• Italian: curva di Bézier f
• Japanese: ベジェ曲線 (Beje kyokusen)
• Russian: крива́я Безье́ f (krivája Bezʹjé)
• Spanish: curva de Bézier f
• Swedish: Bézier-kurva c

See also

• Bernstein form
• control point
• spline

Further reading

• Bernstein polynomial on Wikipedia.Wikipedia
• De Casteljau's algorithm on Wikipedia.Wikipedia
• Bézier curve on Encyclopedia of Mathematics